

#Lattice meaning free
Also, lattice vibrations interact with free electrons in a conducting solid and give rise to electrical resistance. The wave character of the vibrations is needed, however, to describe heat transport by lattice waves. Because of the short wavelength, the motion of neighboring atoms is essentially uncorrelated, so that for many purposes the vibrations can be regarded as those of independently vibrating atoms, each moving about its average position in three dimensions with average vibrational energy of 3 kT, where k is the Boltzmann constant and T the absolute temperature. See Crystal structure, Vibration, Wave motionĪt room temperature and above, most of the thermal energy resides in the waves of highest frequency. The wavelengths at these highest frequencies are of the order of interatomic spacings. The spectrum of lattice waves ranges from these low frequencies to frequencies of the order of 10 13 Hz, and sometimes even higher. These are progressive waves, and at low frequencies they are the elastic waves in the corresponding anisotropic continuum. In a regular lattice with harmonic forces between atoms, the normal modes of vibrations are lattice waves. Because the atoms are bound not to their average positions but to the neighboring atoms, vibrations of neighbors are not independent of each other. In a crystal, these positions form a regular lattice. (1982), Exactly solved models in statistical mechanics (PDF), London: Academic Press Inc.The oscillations of atoms in a solid about their equilibrium positions. A lattice Λ is a Wick rotated version of the action in quantum field theory.Įxamples Condensed matter physics.Lattice models are also used to simulate the structure and dynamics of polymers.Ī number of lattice models can be described by the following data: More generally, lattice gauge theory and lattice field theory are areas of study. However, digital physics considers nature fundamentally discrete at the Planck scale, which imposes upper limit to the density of information, aka Holographic principle.
An example of a continuum theory that is widely studied by lattice models is the QCD lattice model, a discretization of quantum chromodynamics. Physical lattice models frequently occur as an approximation to a continuum theory, either to give an ultraviolet cutoff to the theory to prevent divergences or to perform numerical computations. The solution of these models has given insights into the nature of phase transitions, magnetization and scaling behaviour, as well as insights into the nature of quantum field theory.
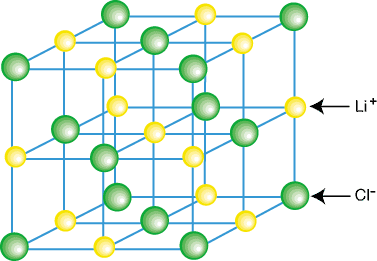
Techniques for solving these include the inverse scattering transform and the method of Lax pairs, the Yang–Baxter equation and quantum groups. The exact solution to many of these models (when they are solvable) includes the presence of solitons. Lattice models are also ideal for study by the methods of computational physics, as the discretization of any continuum model automatically turns it into a lattice model. Some models are exactly solvable, and thus offer insight into physics beyond what can be learned from perturbation theory. Currently, lattice models are quite popular in theoretical physics, for many reasons. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattices such as this are used - for example - in the Flory–Huggins solution theory A three-dimensional lattice filled with two molecules A and B, here shown as black and white spheres.


 0 kommentar(er)
0 kommentar(er)
